FINITE ELEMENT ANALYSIS IN STRUCTURAL MECHANICS
Finite Element Analysis in Structural Mechanics
Finite Element Analysis (FEA) is a powerful numerical technique used in structural mechanics to simulate and analyze the behavior of complex structures. This method breaks down a complex structure into smaller, simpler elements, allowing engineers to gain insights into its performance under various conditions. FEA has become an indispensable tool in the design and analysis of structures across various industries, including civil engineering, aerospace, and automotive. In this article, we will explore the key points of Finite Element Analysis in structural mechanics.
Key Concepts
1. Element Discretization
The core principle of FEA involves dividing a complex structure into finite elements. These elements can take various shapes, such as triangles, quadrilaterals, or tetrahedra in 2D and 3D analyses. This discretization process simplifies the problem, making it computationally manageable while maintaining accuracy.
2. Mathematical Formulation
Once the structure is discretized, the next step is to formulate mathematical equations that describe the behavior of each element. These equations typically involve fundamental principles of mechanics, such as equilibrium equations, constitutive relationships, and compatibility conditions.
3. Assembly of Global Equations
After obtaining element-level equations, they are assembled to create a global system of equations that describes the entire structure. This system of equations represents the structure’s response to external forces and boundary conditions.
4. Solution Techniques
Solving the global system of equations can be a computationally intensive task, especially for large and complex structures. Various solution techniques, including direct solvers and iterative methods, are used to obtain the displacements, stresses, and strains within the structure.
5. Visualization and Post-Processing
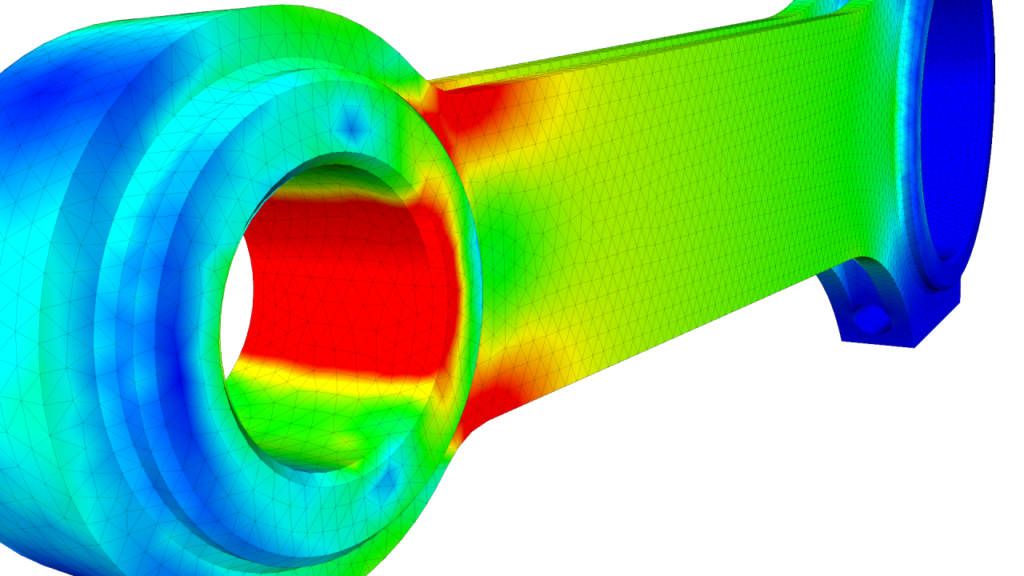
FEA software provides engineers with tools to visualize and interpret the results. Post-processing includes generating contour plots, deformation animations, and stress distribution maps to help engineers make informed decisions about the structure’s performance.
Applications
FEA is widely used in various industries for structural analysis and design:
1. Civil Engineering
In civil engineering, FEA is employed to assess the structural integrity of bridges, buildings, and dams. It helps engineers optimize designs, analyze load-bearing capacity, and ensure safety and reliability.
2. Aerospace and Automotive
In the aerospace and automotive sectors, FEA is crucial for designing lightweight, high-performance structures. It aids in optimizing component shapes and materials, reducing weight, and enhancing fuel efficiency.
3. Mechanical Engineering
FEA is extensively used in mechanical engineering to evaluate the performance of machine components, such as gears, springs, and bearings. It assists in predicting failures, optimizing designs, and improving product reliability.
4. Biomechanics
Biomechanics researchers use FEA to study the mechanics of bones, tissues, and implants. It helps in understanding injury mechanisms and designing medical devices like prosthetics and orthopedic implants.
Advantages of FEA
1. Cost-Efficiency
FEA allows engineers to test and optimize designs in a virtual environment, reducing the need for costly physical prototypes and experiments.
2. Complex Geometry Handling
FEA can handle complex geometries that are difficult to analyze using traditional analytical methods, making it suitable for intricate and unconventional structures.
3. Parametric Studies
Engineers can easily perform parametric studies by changing input variables and studying their impact on the structure’s behavior, enabling efficient design optimization.
Limitations of FEA
1. Assumptions and Simplifications
FEA requires assumptions and simplifications in the mathematical models, which may lead to inaccuracies if not carefully chosen.
2. Mesh Dependency
The accuracy of FEA results depends on the quality and density of the mesh. Inadequate mesh refinement can lead to errors.
3. High Computational Demands
Analyzing large and complex structures can be computationally intensive, necessitating powerful computers and significant computation time.
In conclusion, Finite Element Analysis is an indispensable tool in structural mechanics that allows engineers to analyze and optimize the behavior of complex structures. By breaking down these structures into smaller elements and employing mathematical formulations, FEA has revolutionized the way we design and assess structures across various industries. While it offers numerous advantages, engineers should be aware of its limitations to ensure accurate and reliable results in their analyses and designs.